Tellurium-128 undergoes beta-decay with a half-life estimated to be 77 x 10 24 years. After 5 periods it will be 125132 th.

Ielts Writing Ielts Writing Ielts Ielts Writing Task 2
This lesson explains that process defines important terms such.

. It has a half-life of 123 y. Some isotopes have very short half-lives for example oxygen-14 has a half-life of only 71 seconds some are even shorter with values measured in millionths of a second not being uncommon. Here are some examples.
Tfrac12 0693 λ tfrac12 06930002 3465. The term is also used more generally to characterize any type of exponential or non-exponential decay. For example cobalt-60 an isotope that emits gamma rays used to treat cancer has a half-life of 527 years Figure 115.
Describe how half-life is used to determine the geologic age of a rock. In next 5730 years it will remain 25 grams. So every half-life period t_12 the activity halves from the start of that period.
As radioactive isotopes of elements decay they lose their radioactivity and become a brand new element known as a daughter isotope. See Below It is mostly used for radioactive decay. Half-life is the time required for a quantity to reduce to half of its initial value.
Among the non-generating radioactive isotopes are potassium-40 K-40 with a half-life of 127 billion years old rubidium-87 Rb-87 with a half-life of 475 billion years and about 10 other nuclides that have a half-life of more than 10 billion years. Half-life is the time it takes for half the population of a sample to change into something else. The quantities available here are λ 0002 1years Consequently the half life equation becomes.
The latter has a half-life of only 88 minutes and. It follows that all CRE ages would then shift. Half-life is defined as the time it takes for one-half of a radioactive element to decay into a daughter isotope.
Half life is the time in which a substance remains halve of its original amount. 17 32 053125 displaystyle 1732053125 this is the decimal amount that remains 1 2 n 053125 displaystyle 12n053125. Suppose we have 1000 g of 3 H tritium a radioactive isotope of hydrogen.
The half-life must find its mate or after a few brief days it dies leaving its line extinct. For example at this writing October 2006 the half-lives of 10 Be and of 53 Mn are under active scrutiny. What must be true of that material in order to use half-life to date it.
Describe how half-life might be useful in determining the age of a geological sample. It is unaffected by conditions and is independent of the initial amount of that isotope. Mostly we use the term half life for radioactive substances.
So when an isotope is unstable in its nucleus because of too many neutrons for example the atom will undergo a process that alters the nucleus number of protons and electrons. By measuring the ratio of the amount of the original radioactive element to the daughter isotope scientists can determine how many. So in our example after the second life is over thats 10 years since each half life is 5 years there will be frac 1 2 of 50 of the substance left which of course is 25.
In a given cobalt-60 source since half of the Co 27 60 nuclei decay every 527 years both the amount of material and the intensity of the radiation emitted is cut in half every 527 years. So if we take 100 grams of carbon-14 then it will remain 50 grams in 5730 years. For example- Half life of carbon-14 is 5730 years.
An example is bismuth-209. So if you take ambien after 2 hours the plasma concentration will be reduced to half after 2 more hours the remaining blood levels will be reduced by another half - so a quarter will be left. Scientists use the amount of time it takes for half of an isotope to react or decay or half-life of carbon-14 in carbon dating experiments to determine the age of substances.
The half-life of Ambien is about 2 hours. This latter figure is. Carbon-14 if left by itself will have a half-life of 5730 years wikipedia.
Bismuth-209 is a stable radioactive isotope that undergoes alpha-decay but has a half-life of 19 x 10 19 years which is more than a billion times longer than the estimated age of the universe. Consider the following example. A Geiger counter is an instrument that measures the amount of radioactivity in a sample.
This means that after 5 periods 28650 years it will have only 132th. For example the medical sciences refer to the. The half-life of a specific radioactive isotope is constant.
So after the second period activity will be one half of one half or one quarter of the original. The half-life is defined as the amount of time it takes for a given isotope to lose half of its radioactivity. A radioactive isotope decayed to 1732 of its original mass after 60 minutes.
As was written radioactive decay is a random process at the level of single. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable atoms survive. Solved Examples on Half Life Formula.
Will a Geiger counter show more radioactivity from a sample with a short half-life. Literally half of the substance is gone every five years the half life of this particular substance. The spontaneous transformation of an unstable atomic nucleus into a lighter one in which radiation is released in the form of alpha particles beta particles gamma rays and.
Scientists use a process called radiometric dating to help determine the age of rocks and other objects. One of the most useful terms for estimating how quickly a nuclide will decay is the radioactive half-life t12. Half-life is used to estimate how long it takes for a drug to be removed from your body.
Solved Examples for Half Life Formula. Half-Life Calculation Example. Calculate the half-life of a radioactive substance whose disintegration constant happens to be 0002 1years.
Thats what half life means. In all cases the absolute production rates depend inversely on the half-life of the radionuclide of interest. Thus an increase of 10 in the half-life of 81 Kr would decrease by 10 any value of P s based on 81 Kr measurements.
Calculate the half-life of a radioactive substance whose disintegration constant happens to be 0002 per year. The quantities available here are lambda 0002 per year Consequently the half-life equation becomes. Find the half-life of this radioisotope.
Other elements isotopes can have a much longer half-life thallium-232 has a half-life of 14 10 10 years and carbon-14 has a half-life of 5730 years.

Radioactive Decay And Half Life Science Teaching Resources Chemistry Worksheets Teaching Chemistry

How To Describe A Cycle In Ielts Academic Writing Task 1 Ielts Essay Writing Examples Essay Writing Skills
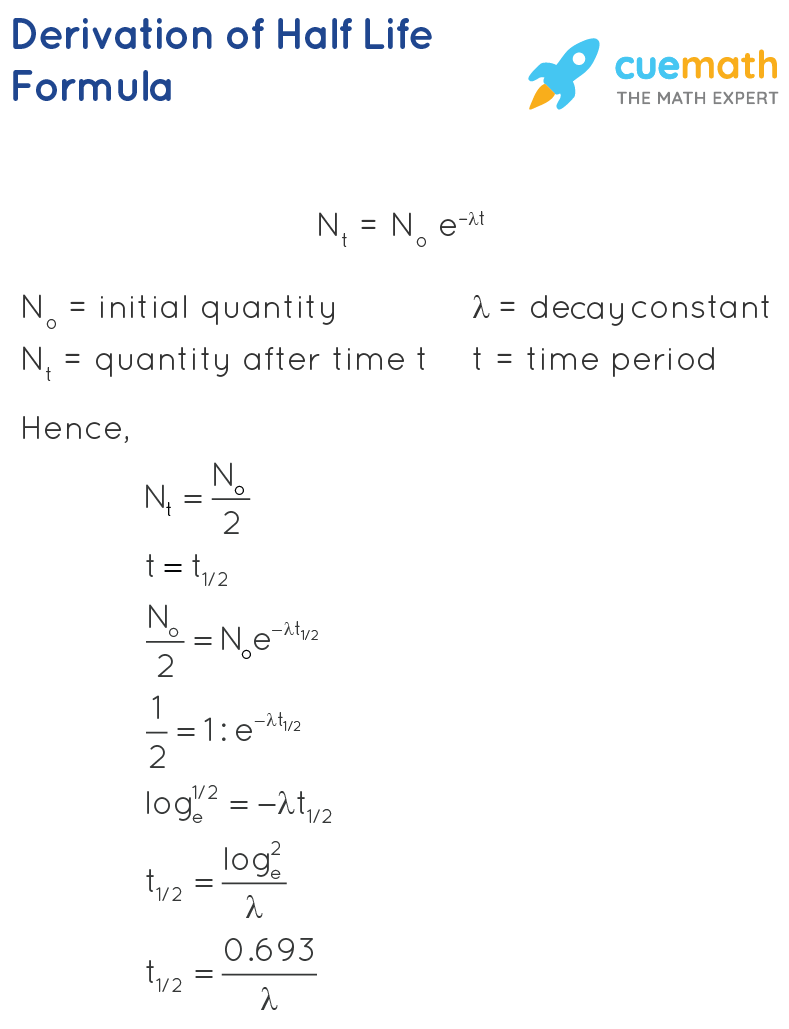
0 Comments